Estimated Losses in Fires in Toronto,Canada
In this project we want to calculate the monthly estimated losses caused by fires that occur in Toronto. We will use the theory of Loss Distributions, in which we will try to find the severity and frequency. The intention of projects like this is to have a confidence margin, usually 95 or 99 percent, in which we are sure that 95% of the time the losses will not exceed this value and if it does exceed it, we can calculate another estimator. These estimators in Risk Theory are known as the Value at Risk (VaR) and the Conditional Value at Risk (CVaR) respectively. The database is taken from: https://open.toronto.ca/dataset/fire-incidents/
We will use the best known distributions for frequency such as the Poisson, the Negative Binomial or the Uniform and to severity, we have a range of possibilities. The first is to use the empirical distribution. Theoretically, we know that there are different known distributions, such as normal, log-normal, Gamma, Exponential, among others. Additionally, we can use distributions that are known to be heavy-tailed, such as Weibull or Generalized Pareto.
The Data
We have the advantage that the data is loaded in the R environment, therefore we will use the official package provided by open data in Toronto.
## # A tibble: 1 x 11
## title id topics civic_issues publisher excerpt dataset_category
## <chr> <chr> <chr> <chr> <chr> <chr> <chr>
## 1 Fire Incidents 64a2669~ Publi~ <NA> Fire Ser~ "This ~ Table
## # ... with 4 more variables: num_resources <int>, formats <chr>,
## # refresh_rate <chr>, last_refreshed <date>| _id | Area_of_Origin | Building_Status | Business_Impact | Civilian_Casualties | Count_of_Persons_Rescued | Estimated_Dollar_Loss | Estimated_Number_Of_Persons_Displaced | Exposures | Ext_agent_app_or_defer_time | Extent_Of_Fire | Final_Incident_Type | Fire_Alarm_System_Impact_on_Evacuation | Fire_Alarm_System_Operation | Fire_Alarm_System_Presence | Fire_Under_Control_Time | Ignition_Source | Incident_Number | Incident_Station_Area | Incident_Ward | Initial_CAD_Event_Type | Intersection | Last_TFS_Unit_Clear_Time | Latitude | Level_Of_Origin | Longitude | Material_First_Ignited | Method_Of_Fire_Control | Number_of_responding_apparatus | Number_of_responding_personnel | Possible_Cause | Property_Use | Smoke_Alarm_at_Fire_Origin | Smoke_Alarm_at_Fire_Origin_Alarm_Failure | Smoke_Alarm_at_Fire_Origin_Alarm_Type | Smoke_Alarm_Impact_on_Persons_Evacuating_Impact_on_Evacuation | Smoke_Spread | Sprinkler_System_Operation | Sprinkler_System_Presence | Status_of_Fire_On_Arrival | TFS_Alarm_Time | TFS_Arrival_Time | TFS_Firefighter_Casualties |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 526081 | 81 - Engine Area | NA | NA | 0 | 0 | 15000 | NA | NA | 2018-02-24T21:12:00 | NA | 01 - Fire | NA | NA | NA | 2018-02-24T21:15:40 | 999 - Undetermined | F18020956 | 441 | 1 | Vehicle Fire | Dixon Rd / 427 N Dixon Ramp | 2018-02-24T21:38:31 | 43.68656 | NA | -79.59942 | 47 - Vehicle | 1 - Extinguished by fire department | 1 | 4 | 99 - Undetermined | 896 - Sidewalk, street, roadway, highway, hwy (do not use for fire incidents) | NA | NA | NA | NA | NA | NA | NA | 7 - Fully involved (total structure, vehicle, spreading outdoor fire) | 2018-02-24T21:04:29 | 2018-02-24T21:10:11 | 0 |
| 526082 | 75 - Trash, rubbish area (outside) | NA | NA | 0 | 0 | 50 | NA | NA | 2018-02-24T21:29:42 | NA | 01 - Fire | NA | NA | NA | 2018-02-24T21:32:24 | 999 - Undetermined | F18020969 | 116 | 18 | Fire - Grass/Rubbish | Sheppard Ave E / Clairtrell Rd | 2018-02-24T21:35:58 | 43.76613 | NA | -79.39004 | 97 - Other | 1 - Extinguished by fire department | 1 | 4 | 03 - Suspected Vandalism | 896 - Sidewalk, street, roadway, highway, hwy (do not use for fire incidents) | NA | NA | NA | NA | NA | NA | NA | 2 - Fire with no evidence from street | 2018-02-24T21:24:43 | 2018-02-24T21:29:31 | 0 |
| 526083 | NA | NA | NA | 0 | 0 | NA | NA | NA | NA | NA | 03 - NO LOSS OUTDOOR fire (exc: Sus.arson,vandal,child playing,recycling or dump fires) | NA | NA | NA | NA | NA | F18021182 | 221 | 21 | Fire - Highrise Residential | Danforth Rd / Savarin St | 2018-02-25T14:14:03 | 43.74323 | NA | -79.24506 | NA | NA | 6 | 22 | NA | 891 - Outdoor general auto parking | NA | NA | NA | NA | NA | NA | NA | NA | 2018-02-25T13:29:59 | 2018-02-25T13:36:49 | 0 |
| 526084 | 75 - Trash, rubbish area (outside) | 01 - Normal (no change) | 1 - No business interruption | 0 | 0 | 0 | 0 | NA | 2018-02-25T14:19:25 | 1 - Confined to object of origin | 01 - Fire | 9 - Undetermined | 8 - Not applicable (no system) | 9 - Undetermined | 2018-02-25T14:20:00 | 999 - Undetermined | F18021192 | 133 | 5 | Fire - Commercial/Industrial | Keele St / Lawrence Ave W | 2018-02-25T15:07:42 | 43.70866 | 999 | -79.47806 | 99 - Undetermined (formerly 98) | 1 - Extinguished by fire department | 6 | 22 | 99 - Undetermined | 511 - Department Store | 9 - Floor/suite of fire origin: Smoke alarm presence undetermined | 98 - Not applicable: Alarm operated OR presence/operation undetermined | 9 - Type undetermined | 8 - Not applicable: No alarm, no persons present | 99 - Undetermined | 8 - Not applicable - no sprinkler system present | 9 - Undetermined | 3 - Fire with smoke showing only - including vehicle, outdoor fires | 2018-02-25T14:13:39 | 2018-02-25T14:18:07 | 0 |
| 526085 | NA | NA | NA | 0 | 0 | NA | NA | NA | NA | NA | 03 - NO LOSS OUTDOOR fire (exc: Sus.arson,vandal,child playing,recycling or dump fires) | NA | NA | NA | NA | NA | F18021271 | 132 | 8 | Fire - Residential | Replin Rd / Tapestry Lane | 2018-02-25T18:34:24 | 43.71812 | NA | -79.44318 | NA | NA | 6 | 22 | NA | 860 - Lawn around structure | NA | NA | NA | NA | NA | NA | NA | NA | 2018-02-25T18:20:43 | 2018-02-25T18:26:19 | 0 |
| 526086 | 81 - Engine Area | NA | NA | 0 | 0 | 1500 | NA | NA | 2018-02-25T18:38:00 | NA | 01 - Fire | NA | NA | NA | 2018-02-25T18:40:00 | 999 - Undetermined | F18021274 | 215 | 25 | Vehicle Fire | Lawrence Ave E / Beechgrove Dr | 2018-02-25T19:08:28 | 43.77379 | NA | -79.16228 | 47 - Vehicle | 1 - Extinguished by fire department | 7 | 25 | 99 - Undetermined | 837 - Vehicles or Vehicle Parts | NA | NA | NA | NA | NA | NA | NA | 4 - Flames showing from small area (one storey or less, part of a vehicle, outdoor) | 2018-02-25T18:31:19 | 2018-02-25T18:35:17 | 0 |
| 526087 | 22 - Sleeping Area or Bedroom (inc. patients room, dormitory, etc) | 01 - Normal (no change) | 1 - No business interruption | 0 | 0 | 2000 | 0 | NA | 2018-02-26T18:28:00 | 2 - Confined to part of room/area of origin | 01 - Fire | 8 - Not applicable: No fire alarm system, no persons present | 8 - Not applicable (no system) | 8 - Not applicable (bldg not classified by OBC OR detached/semi/town home) | 2018-02-26T18:30:00 | 51 - Incandescent Lamp - Light Bulb, Spotlight | F18021633 | 235 | 19 | Fire - Residential | Westview Blvd / Holland Ave | 2018-02-26T19:05:58 | 43.71481 | 002 | -79.30411 | 16 - Insulation | 1 - Extinguished by fire department | 6 | 22 | 20 - Design/Construction/Installation/Maintenance Deficiency | 301 - Detached Dwelling | 1 - Floor/suite of fire origin: No smoke alarm | 98 - Not applicable: Alarm operated OR presence/operation undetermined | 8 - Not applicable - no smoke alarm or presence undetermined | 7 - Not applicable: Occupant(s) first alerted by other means | 2 - Confined to part of room/area of origin | 8 - Not applicable - no sprinkler system present | 3 - No sprinkler system | 2 - Fire with no evidence from street | 2018-02-26T18:18:55 | 2018-02-26T18:24:47 | 0 |
| 526088 | 55 - Mechanical/Electrical Services Room | 01 - Normal (no change) | 2 - May resume operations within a week | 0 | 0 | 100000 | 0 | NA | 2018-02-27T10:57:32 | 2 - Confined to part of room/area of origin | 01 - Fire | 2 - Some persons (at risk) evacuated as a result of hearing fire alarm system | 1 - Fire alarm system operated | 1 - Fire alarm system present | 2018-02-27T11:36:09 | 23 - Distribution Equipment (includes panel boards, fuses, circuit br | F18021837 | 231 | 24 | Alarm Highrise Residential | Peking Rd / Nelson St | 2018-02-27T13:51:29 | 43.74858 | 011 | -79.22237 | 43 - Electrical Wiring Insulation | 1 - Extinguished by fire department | 24 | 71 | 52 - Electrical Failure | 323 - Multi-Unit Dwelling - Over 12 Units | 9 - Floor/suite of fire origin: Smoke alarm presence undetermined | 98 - Not applicable: Alarm operated OR presence/operation undetermined | 8 - Not applicable - no smoke alarm or presence undetermined | 2 - Some persons (at risk) self evacuated as a result of hearing alarm | 7 - Spread to other floors, confined to building | 8 - Not applicable - no sprinkler system present | 3 - No sprinkler system | 2 - Fire with no evidence from street | 2018-02-27T10:28:12 | 2018-02-27T10:35:13 | 0 |
| 526089 | 28 - Office | 01 - Normal (no change) | 1 - No business interruption | 0 | 0 | 5000 | 0 | NA | 2018-02-25T15:57:00 | 1 - Confined to object of origin | 01 - Fire | 1 - All persons (at risk of injury) evacuated as a result of hearing fire alarm system | 1 - Fire alarm system operated | 1 - Fire alarm system present | 2018-02-25T15:58:00 | 41 - Other Heating Equipment | F18021221 | 332 | 10 | Alarm Commercial/Industrial | Bay St | 2018-02-25T19:55:41 | 43.65215 | 003 | -79.38234 | 56 - Paper, Cardboard | 1 - Extinguished by fire department | 8 | 20 | 46 - Used or Placed too close to combustibles | 156 - Court Facility | 2 - Floor/suite of fire origin: Smoke alarm present and operated | 98 - Not applicable: Alarm operated OR presence/operation undetermined | 2 - Hardwired (standalone) | 1 - All persons (at risk of injury) self evacuated as a result of hearing alarm | 4 - Spread beyond room of origin, same floor | 3 - Did not activate: fire too small to trigger system | 1 - Full sprinkler system present | 4 - Flames showing from small area (one storey or less, part of a vehicle, outdoor) | 2018-02-25T15:48:34 | 2018-02-25T15:52:04 | 0 |
| 526090 | NA | NA | NA | 0 | 0 | NA | NA | NA | NA | NA | 03 - NO LOSS OUTDOOR fire (exc: Sus.arson,vandal,child playing,recycling or dump fires) | NA | NA | NA | NA | NA | F18021565 | 426 | 4 | Vehicle Fire | Roncesvalles Ave / Dundas St W | 2018-02-26T15:57:48 | 43.65388 | NA | -79.45185 | NA | NA | 1 | 4 | NA | 901 - Automobile | NA | NA | NA | NA | NA | NA | NA | NA | 2018-02-26T15:32:11 | 2018-02-26T15:37:40 | 0 |
There are a total of 17536 observations. We have many variables that for this particular analysis we will not take. We will only focus on “Estimated_Dollar_Loss and”TFS_Alarm_Time”, this because they adapt to the study we want to do. An important consideration is the time of the fire, because we have different variables that measure when the alarm originated, when the place was reached or when it was controlled. For practical purposes we will take the time when the alarm noticed that the fire started, in future analysis could take another direction regarding this issue.
Additionally, we have values in losses that are NA or 0, for our study, we will eliminate these observations.
## 'data.frame': 13571 obs. of 2 variables:
## $ LossDolar: int 15000 50 1500 2000 100000 5000 500 7000 15000 60000 ...
## $ Time : Date, format: "2018-02-24" "2018-02-24" ...Therefore for our project we will have a total of 13571 observations.
Frequency Distribution
To find the frequency distribution, wemake a monthly grouping of the events, this is visualized in the following graph.
From this graph we find that the distribution is very similar to a uniform,but we will use all the tools to find which is the distribution that best fits.
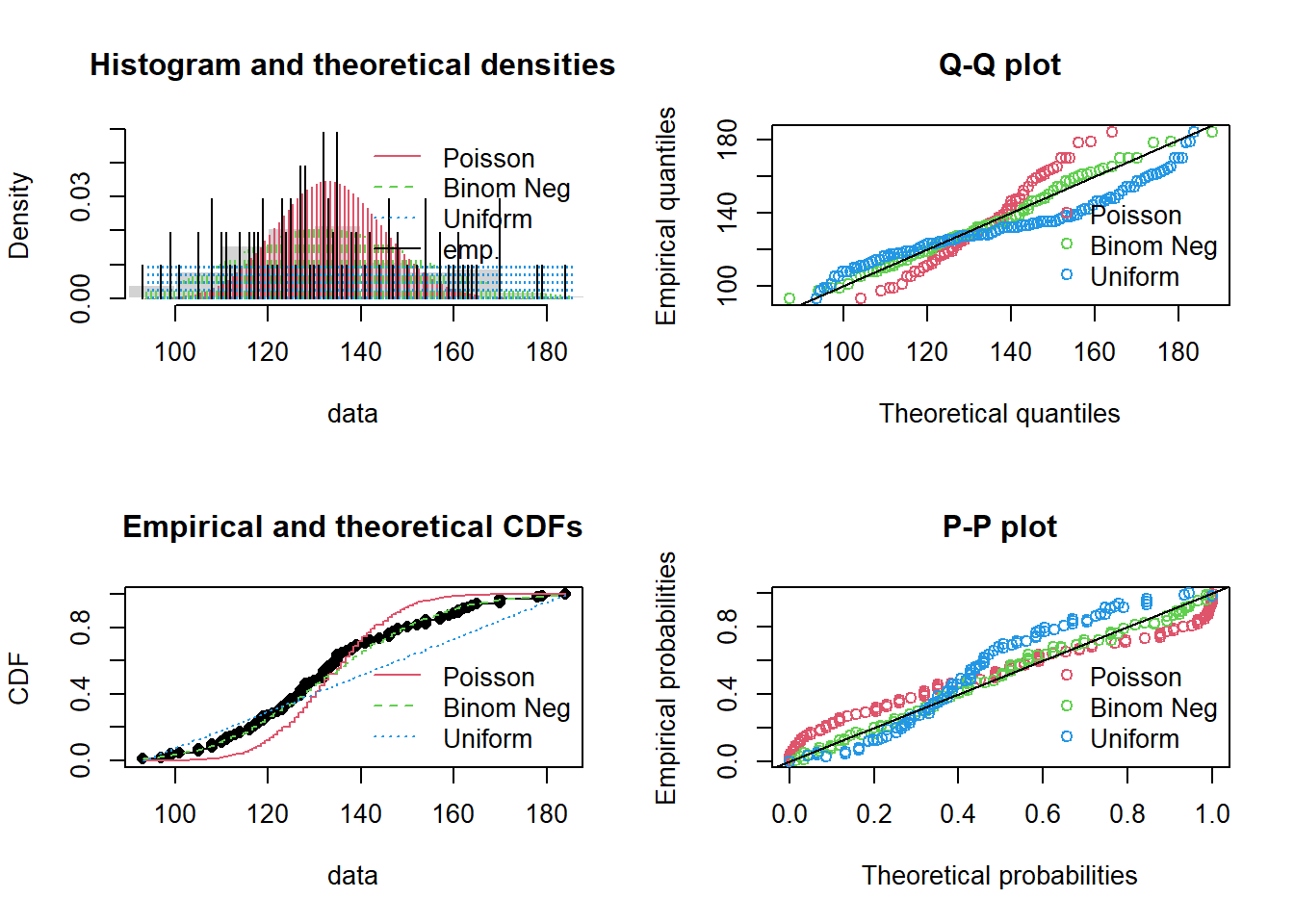
## Chi-squared statistic: 136.7653 4.77875 37.94487
## Degree of freedom of the Chi-squared distribution: 8 7 7
## Chi-squared p-value: 1.116028e-25 0.6869424 3.104186e-06
## the p-value may be wrong with some theoretical counts < 5
## Chi-squared table:
## obscounts theo 1-mle-pois theo 2-mle-nbinom theo 3-mle-unif
## <= 108 10 1.475611 10.027779 16.813187
## <= 116 10 6.005402 10.392029 8.967033
## <= 121 9 8.662435 8.652967 5.604396
## <= 125 9 10.282219 7.818023 4.483516
## <= 128 9 9.395659 6.186942 3.362637
## <= 133 11 17.355863 10.486356 5.604396
## <= 137 9 13.605855 8.150595 4.483516
## <= 146 11 22.699495 15.998408 10.087912
## <= 157 10 10.572665 13.273201 12.329670
## > 157 14 1.944796 11.013700 30.263736
##
## Goodness-of-fit criteria
## 1-mle-pois 2-mle-nbinom 3-mle-unif
## Akaike's Information Criterion 978.4313 897.6838 924.2153
## Bayesian Information Criterion 981.0563 902.9337 929.4653Both graphically an the different tests, we found that the distribution that best fits our data is the Negative Binomial, so we will use this to continue with our study.
Severity Distribution
In the case of Severity, we will take 2 different methods, the first one will be try to find the best distribution of the existing ones that we mentioned at the beginning. The second we will use the Generalized Pareto distribution, which is used for events with many extreme values, which will be quite useful for this exercise.
Now just for practical purposes, we will see the behavior prior to the million dollars.
We notice how the majority of the losses events are less than $ 2,500 buy we have long tails of events with losses approaching $ 50 million. It will be difficult to find a distribution that fits our data, but we will continue with the analysis, if necessary we could use a transformation of the data in order to soften a little the effect of those values so distant. Additionally, let’s see how much estimated money is lost monthly to get an idea of what kind of final behavior we should have.
We are going to use the criteria of the AIC and BIC to find the possible best distributions
## distribucion df AIC
## 1 mllnorm(datos$LossDolar) 2 284788.3
## 2 mlweibull(datos$LossDolar) 2 285367.4
## 3 mlgamma(datos$LossDolar) 2 289998.5
## 4 mlbetapr(datos$LossDolar) 2 297923.0
## 5 mlinvgamma(datos$LossDolar) 2 299226.8
## 6 mlinvgauss(datos$LossDolar) 2 313529.5
## 7 mlexp(datos$LossDolar) 1 314958.3
## 8 mlgumbel(datos$LossDolar) 2 334100.1
## 9 mlinvweibull(datos$LossDolar) 2 NaN## distribucion df BIC
## 1 mllnorm(datos$LossDolar) 2 284803.3
## 2 mlweibull(datos$LossDolar) 2 285382.5
## 3 mlgamma(datos$LossDolar) 2 290013.6
## 4 mlbetapr(datos$LossDolar) 2 297938.0
## 5 mlinvgamma(datos$LossDolar) 2 299241.8
## 6 mlpareto(datos$LossDolar) 2 307125.3
## 7 mlinvgauss(datos$LossDolar) 2 313544.6
## 8 mlexp(datos$LossDolar) 1 314965.8
## 9 mlgumbel(datos$LossDolar) 2 334115.1
## 10 mlinvweibull(datos$LossDolar) 2 NaNFrom the AIC and BIC criteria, we see how the lognormal and Weibull distributions are the best to fit our data.

## Goodness-of-fit statistics
## 1-mle-lnorm 2-mle-weibull
## Kolmogorov-Smirnov statistic 0.08387221 0.08820628
## Cramer-von Mises statistic 8.91037439 14.72768401
## Anderson-Darling statistic 51.22907343 Inf
##
## Goodness-of-fit criteria
## 1-mle-lnorm 2-mle-weibull
## Akaike's Information Criterion 284788.3 285367.4
## Bayesian Information Criterion 284803.3 285382.5We noticed that there are problems with both distributions, but the normal log still stands out better.
Data Transformation
As we mentioned before, having such high values, one way to smooth these data is to take a transformation, for this case we will only use the logarithmic transformation, additionally we will filter those lost that are 1, because when using this transformation, working with 0 it gets complicated.
## distribucion df AIC
## 1 mlweibull(datos2$LossDolar) 2 59840.34
## 2 mlgamma(datos2$LossDolar) 2 61439.15
## 3 mllnorm(datos2$LossDolar) 2 63077.67
## 4 mlinvgauss(datos2$LossDolar) 2 63777.18
## 5 mlbetapr(datos2$LossDolar) 2 64846.83
## 6 mlinvgamma(datos2$LossDolar) 2 65971.70
## 7 mlinvweibull(datos2$LossDolar) 2 72936.35
## 8 mlexp(datos2$LossDolar) 1 83749.92
## 9 mlgumbel(datos$LossDolar) 2 334100.06## distribucion df BIC
## 1 mlweibull(datos2$LossDolar) 2 59855.35
## 2 mlgamma(datos2$LossDolar) 2 61454.17
## 3 mlgumbel(datos2$LossDolar) 2 62750.45
## 4 mllnorm(datos2$LossDolar) 2 63092.69
## 5 mlinvgauss(datos2$LossDolar) 2 63792.19
## 6 mlbetapr(datos2$LossDolar) 2 64861.84
## 7 mlinvgamma(datos2$LossDolar) 2 65986.71
## 8 mlinvweibull(datos2$LossDolar) 2 72951.36
## 9 mlexp(datos2$LossDolar) 1 83757.43
## 10 mlpareto(datos2$LossDolar) 2 106525.73From the AIC and BIC criteria, we see how the Weibull and Gamma distributions are the best to fit our data.

## Goodness-of-fit statistics
## 1-mle-weibull 2-mle-gamma
## Kolmogorov-Smirnov statistic 0.06647409 0.1132842
## Cramer-von Mises statistic 5.20233377 24.1283028
## Anderson-Darling statistic 27.29902607 141.1293892
##
## Goodness-of-fit criteria
## 1-mle-weibull 2-mle-gamma
## Akaike's Information Criterion 59840.34 61439.15
## Bayesian Information Criterion 59855.35 61454.17Generalized Pareto
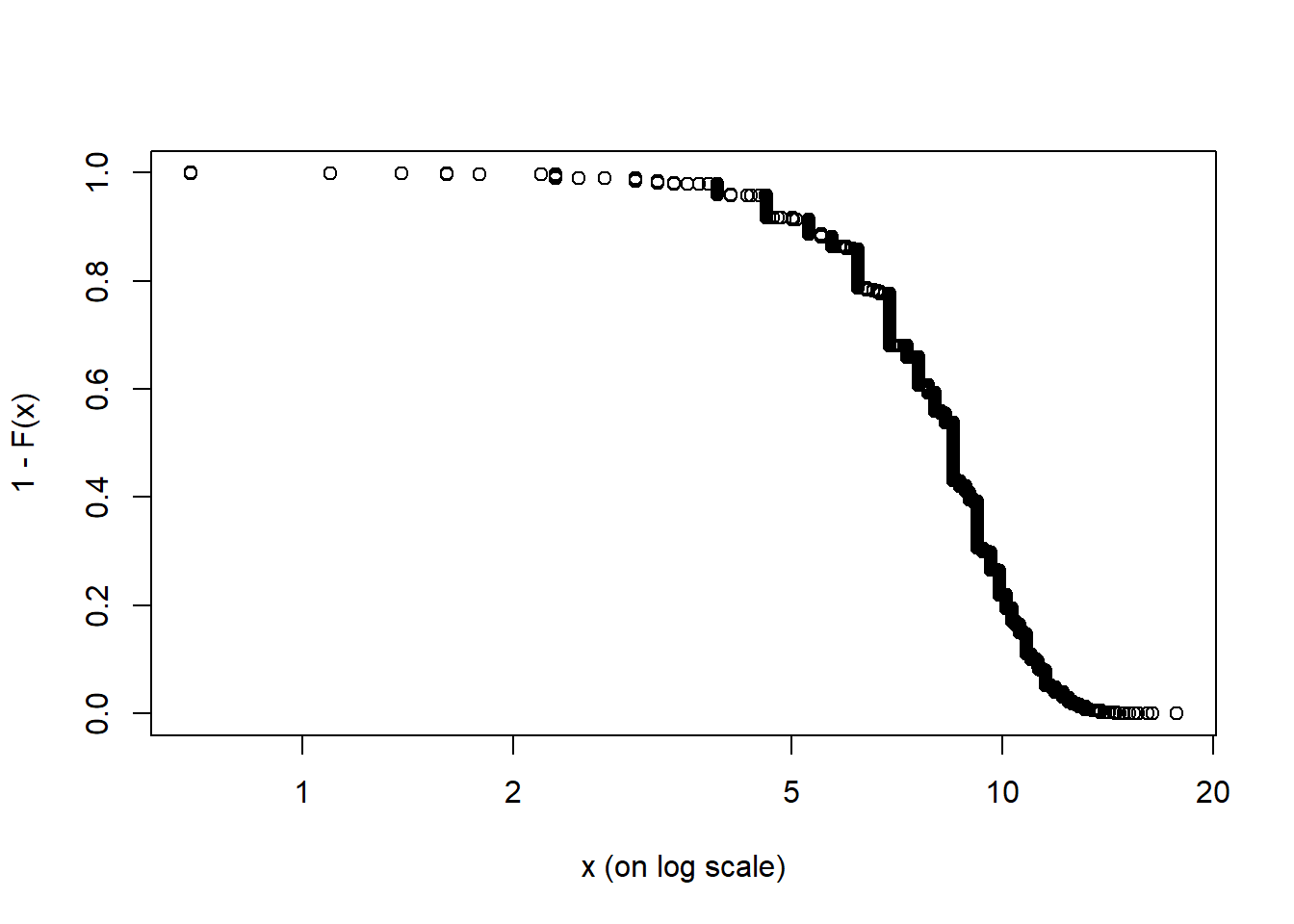
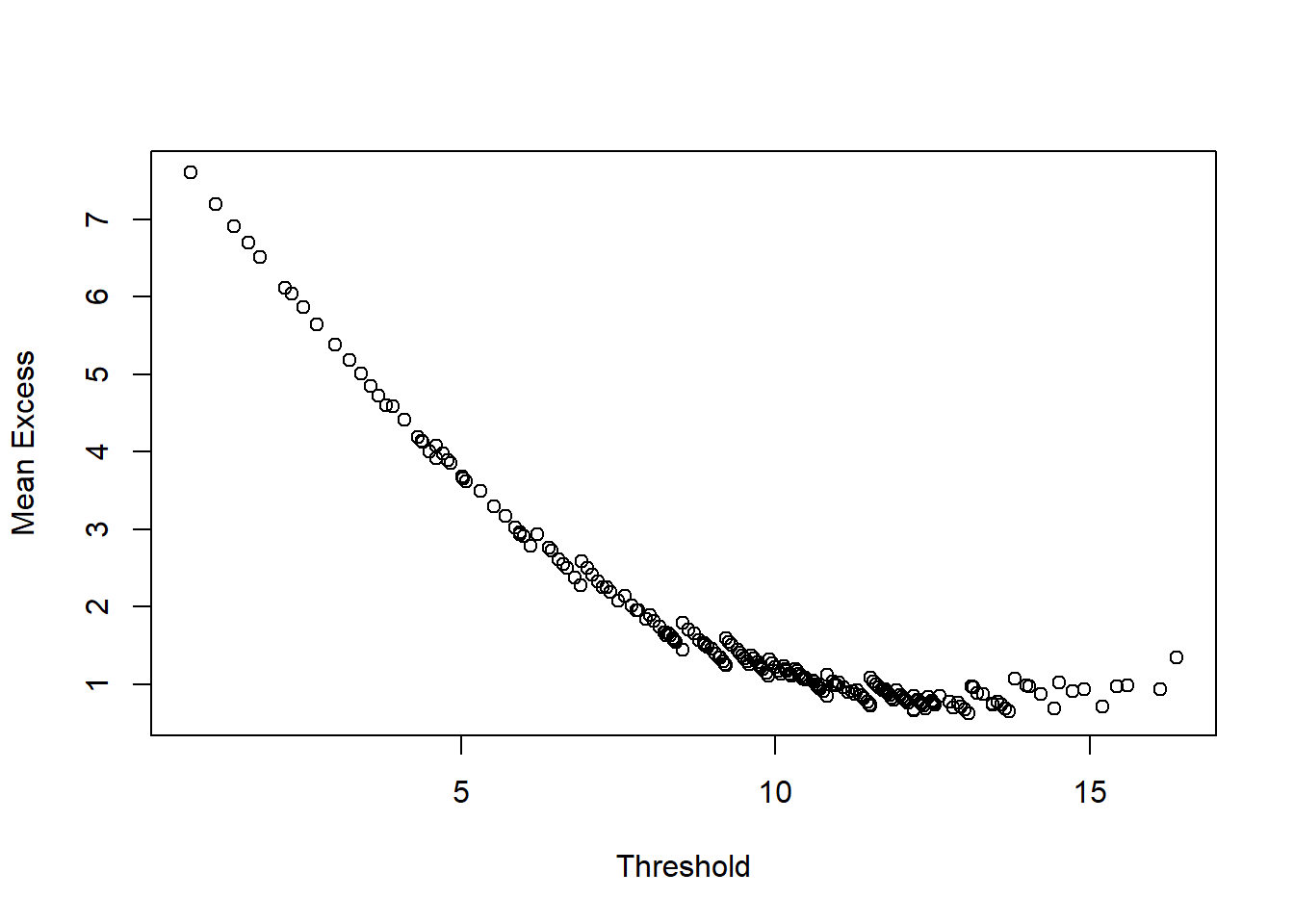

This visually indicates that using the Generalized Pareto could work for this project.
Simulation
Now we know the behavior of the Severity and Frequency, we will continue with the simulation of the event, this uses the convulsion theory, in which it allows us to combine these 2 distributions to find a final answer, which will indicate how much money is estimated to lose for fires in the Toronto area. We will take 10 000 simulations.
set.seed(777)
m <- 10000Set a random seed to 777 just to have equal results for loading the document.
Conclusions
Through loss distribution theory, we find how much could be estimated to lose monthly due to fires that occur in Toronto. We try to solve this problem by finding those distributions that best fit both the severity and the frequency of the event. In the case of frequency, there is no doubt that the Negative Binomial distribution is the one that best fits, then for Severity, as we mentioned, we took 2 paths, but before that we decided to transform the data or smooth them to minimize the impact of extreme values, but always being considered in our study, because these have a great importance in our study. We managed to find that the Weibull was the best to adjusted to our data, additionally we approached by the Generalized Pareto distribution, which for cases where the extreme values are so important usually manages to capture them in a good way
| Perdida Esperada | VaR al 95% | CVaR al 95% | |
|---|---|---|---|
| Actual Monthly Data | 5 361 408 | 11 194 679 | 21 824 898 |
| Proyected Weibull | 4 642 012 | 8 111 695 | 10 269 715 |
| Proyected Generalized Pareto | 5 449 758 | 11 048 694 | 16 724 907 |
We first clarify that the values presented with real data are only used to compare how close they are to those found, but they do not necessarily represent the VaR and CVaR in strict terms. What we see is that the Weibull underestimates the losses a little with respect to the real data. The Generalized Pareto manages to better capture these losses, reaching results that are very close to the real ones. The monthly losses are estimated to be $5,449,758 on average or it is the expected value, that is, abusing a bit of notation, in a normal average case that amount is what would expect to be the monthly fire lost.
Now, with respect to VaR, the amount is $11,048,694, this means that if we want to cover 95% of the possible cases that could arise in monthly fires, we use this value. Usually in Risk Theory we use values of 95% or 99%, in order to have greater security and cover practically all scenarios. Lastly, we use the CVaR, which is a term more linked to other areas, especially financial ones, because this value is very important in terms of losses, since it tells us, given that we have passed that 95% threshold, how much I estimate to lose in average in these cases. For our exercise, this value represents $16,724,907.
As a final argument, it is important to clarify that the terminology of VaR and CVaR, although they are more linked to other areas, it is also important to measure it in these cases, because for example, an insurer or the state itself must cover it, they must have a base or a security that with an estimated amount can cover practically 95% of the cases. Also be sure that in those months that this threshold is passed we also have defined a value that realistically represents how much money we need to cover this situation.